과제 (Optional)
- int 값을 가지고 있는 이진 트리를 나타내는 Node 라는 클래스를 정의하세요.
- int value, Node left, right를 가지고 있어야 합니다.
- BinrayTree라는 클래스를 정의하고 주어진 노드를 기준으로 출력하는 bfs(Node node)와 dfs(Node node) 메소드를 구현하세요.
- DFS는 왼쪽, 루트, 오른쪽 순으로 순회하세요.
트리(tree)
트리를 구성하는 요소는 노드(node)와 가지(edge)입니다.
각각의 노드는 가지를 통해 다른 노드와 연결되어 있습니다.
트리 관련 용어
루트(root)
- 트리의 가장 윗부분에 위치하는 노드. 하나의 트리에는 하나의 루트가 존재
리프(leaf)
- 트리의 가장 아랫부분에 위치하는 노드. 끝 노드(terminal node) 또는 바깥노드(external node) 라고도 합니다
안쪽 노드(non-termival node)
- 루트를 포함하여 리프를 제외한 노드
자식(child)
- 어떤 노드로부터 가지로 연결된 아래쪽 노드. 노드는 자식을 여러개 가질 수 있습니다
부모(parent)
- 어떤 노드에서 가지로 연결된 위쪽 노드. 노드는 1개의 부모를 가집니다. (루트는 부모를 가질 수 없음)
형제(sibling)
- 같은 부모를 가지는 노드
조상(ancestor)
- 어떤 노드에서 가지로 연결된 위쪽 노드
자손(descendant)
- 어떤 노드에서 가지로 연결된 아래쪽 노드
레벨(level)
- 루트로부터 얼마나 떨어져 있는지에 대한 값.
차수(degree)
- 노드가 갖는 자식의 수
높이(height)
- 루트로부터 가장 멀리 떨어진 리프까지의 거리
서브 트리(subtree)
- 트리안에서 다시 어떤 노드를 루트로 정하고 그 자손으로 이루어진 트리를 서브트리
널 트리(null tree)
- 노드, 가지가 없는 트리
이진 트리
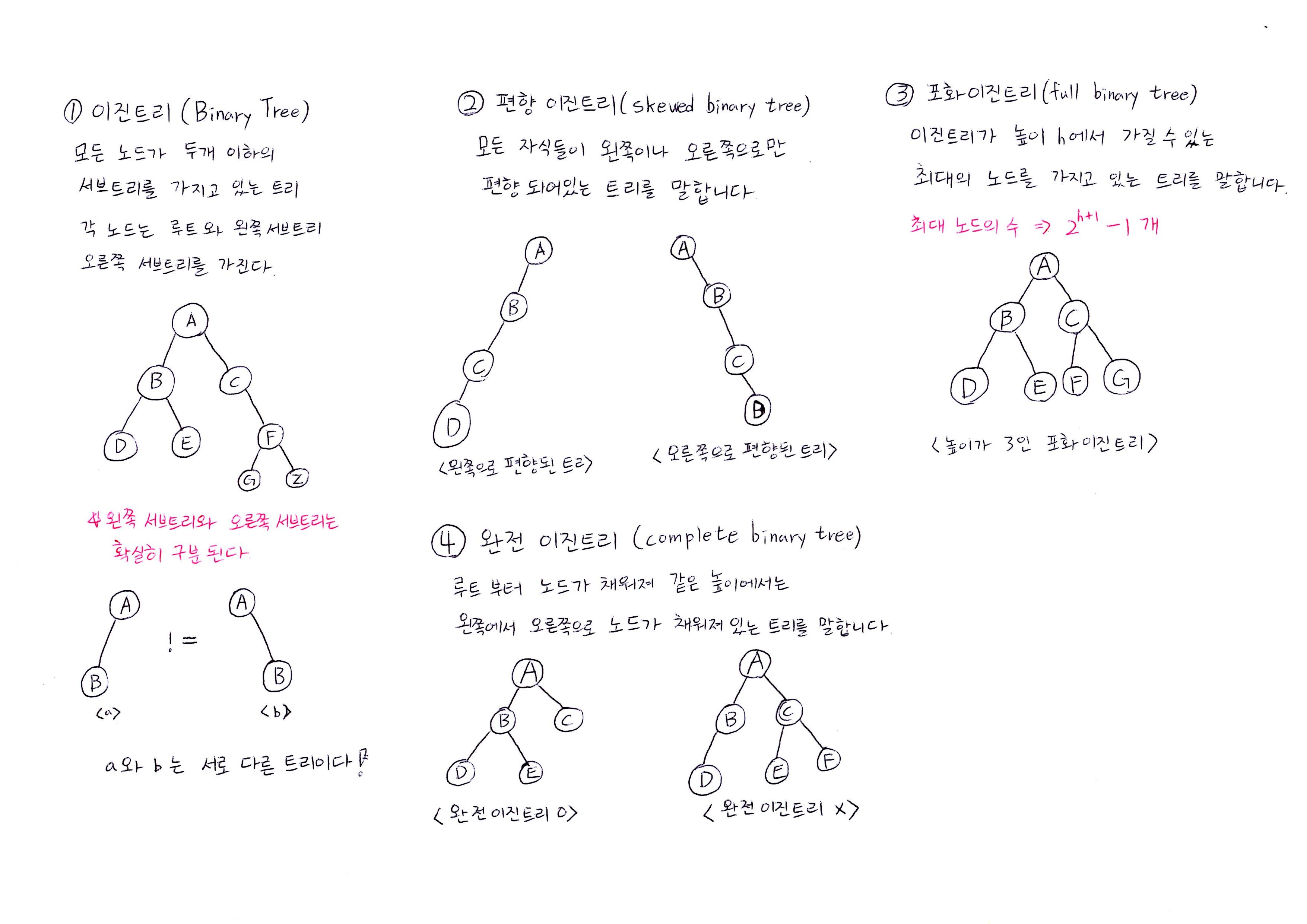
너비우선탐색(BFS)
트리 구조의 낮은 레벨에서부터 시작해서 왼쪽에서 오른쪽 방향으로 검색하고 레벨이 끝나면 다음 레벨로 내려가서 다시 왼쪽에서 오른쪽 방향으로 검색하는 탐색법입니다.
마지막 레벨까지 탐색하면 끝이납니다.
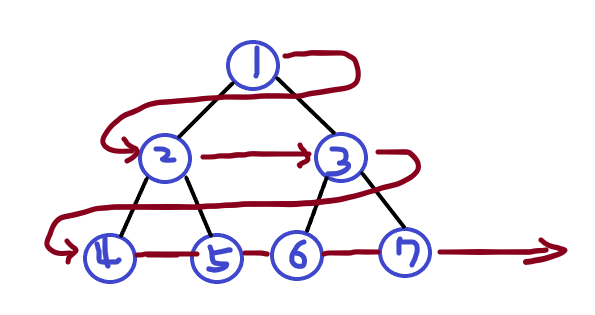
깊이 우선 탐색
리프(가장 마지막 레벨에 있는 노드)까지 내려가는것을 우선순위로 하는 탐색방법
리프에 도달해서 더이상 진행할 곳이 없으면 부모에게 돌아갑니다.
이렇게하면 부모를 여러번 지나가게 되는데 이때 부모를 언제 방문할지 정하는 것으로
깊이 우선 탐색을 3종류로 나눌 수 있습니다.

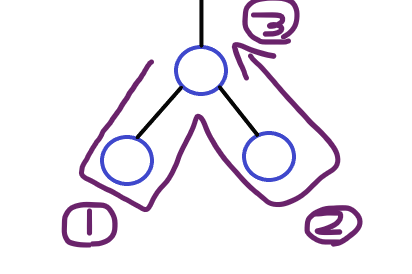
1. 전위 순회(Preorder)
부모노드 -> 왼쪽 자식 -> 부모노드오른쪽 자식

2. 중위 순회(Inorder)
왼쪽 자식 -> 부모노드 -> 오른쪽 자식

3. 후위순회(Postorder)
왼쪽 자식 -> 오른쪽 자식 -> 부모노드 순서로 방문합니다.
Node 클래스
public class Node {
private int value;
private Node left;
private Node right;
public Node(int value) {
this.value = value;
left = null;
right = null;
}
public Node(int value, Node left, Node right) {
this.value = value;
this.left = left;
this.right = right;
}
public void setLeft(Node left) {
this.left = left;
}
public void setRight(Node right) {
this.right = right;
}
public Node getLeft() {
return left;
}
public Node getRight() {
return right;
}
public int getValue() {
return value;
}
public boolean isNullLeft() {
return this.left == null;
}
public boolean isNullRight() {
return this.right == null;
}
}
BinaryTree 클래스
import java.util.*;
import java.util.LinkedList;
public class BinaryTree {
Node root;
public void setRoot(Node root) {
this.root = root;
}
public Node getRoot() {
return root;
}
public List<Integer> bfs(Node node) {
Queue<Node> queue = new LinkedList<>();
List<Integer> result = new ArrayList<>();
queue.add(node);
while (queue.size() != 0) {
Node pollNode = queue.poll();
result.add(pollNode.getValue());
if (!pollNode.isNullLeft()) {
queue.add(pollNode.getLeft());
}
if (!pollNode.isNullRight()) {
queue.add(pollNode.getRight());
}
}
return result;
}
public void preorderDFS(Node node, List<Integer> list) {
list.add(node.getValue());
if (!node.isNullLeft()) {
preorderDFS(node.getLeft(), list);
}
if (!node.isNullRight()) {
preorderDFS(node.getRight(), list);
}
}
public void inorderDFS(Node node, List<Integer> list) {
if (!node.isNullLeft()) {
inorderDFS(node.getLeft(), list);
}
list.add(node.getValue());
if (!node.isNullRight()) {
inorderDFS(node.getRight(), list);
}
}
public void postorderDFS(Node node, List<Integer> list) {
if (node.getLeft() != null) {
postorderDFS(node.getLeft(), list);
}
if (node.getRight() != null) {
postorderDFS(node.getRight(), list);
}
list.add(node.getValue());
}
}
BinaryTreeTest 클래스
import org.junit.jupiter.api.BeforeAll;
import org.junit.jupiter.api.Test;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import static org.junit.jupiter.api.Assertions.*;
public class BinaryTreeTest {
static Node node0;
static Node node1;
static Node node2;
static Node node3;
static Node node4;
static Node node5;
static Node node6;
static Node node7;
static Node node8;
static Node node9;
static Node node10;
static BinaryTree binaryTree = new BinaryTree();
@BeforeAll
static void 이중트리_세팅() {
node10 = new Node(10);
node9 = new Node(9);
node8 = new Node(8);
node7 = new Node(7);
node6 = new Node(6);
node5 = new Node(5);
node4 = new Node(4, node9, node10);
node3 = new Node(3, node7, node8);
node2 = new Node(2, node5, node6);
node1 = new Node(1, node3, node4);
node0 = new Node(0, node1, node2);
binaryTree.setRoot(node0);
}
@Test
public void bfs_테스트() {
List<Integer> bfsResult = binaryTree.bfs(node0);
assertEquals(bfsResult, Arrays.asList(0,1,2,3,4,5,6,7,8,9,10));
}
@Test
public void 전위순회_dfs_테스트() {
List<Integer> bfsResult = new ArrayList<>();
binaryTree.preorderDFS(node0, bfsResult);
assertEquals(bfsResult, Arrays.asList(0,1,3,7,8,4,9,10,2,5,6));
}
@Test
public void 중위순회_dfs_테스트() {
List<Integer> bfsResult = new ArrayList<>();
binaryTree.inorderDFS(node0, bfsResult);
assertEquals(bfsResult, Arrays.asList(7,3,8,1,9,4,10,0,5,2,6));
}
@Test
public void 후위순회_dfs_테스트() {
List<Integer> bfsResult = new ArrayList<>();
binaryTree.postorderDFS(node0, bfsResult);
assertEquals(bfsResult, Arrays.asList(7,8,3,9,10,4,1,5,6,2,0));
}
}
'java-liveStudy' 카테고리의 다른 글
| 7주차. 패키지 (0) | 2021.01.01 |
|---|---|
| 6주차 과제. 상속 (0) | 2020.12.25 |
| 5주차. 클래스 (0) | 2020.12.16 |
| 4주차 과제. 제어문 + 과제 (0) | 2020.12.04 |
| 3주차 과제. 연산자 (0) | 2020.11.26 |




댓글