- 데이터 단위와 자료구조
- Array and LinkedList
- Stack and Queue
- Sort
데이터 단위와 자료구조
데이터 단위
- 데이터를 구성하는 한 덩어리 라고 생각하시면 됩니다.
자료구조(data-structure)
- 자료를 효율적으로 이용할 수 있도록 컴퓨터에 저장하는것을 말합니다.
Array and LinkedList
Array
가장 기본적이고 간단한 자료구조인 Array는 논리적 저장 순서와 물리적 저장 순서가 일치합니다. 인덱스(Index) 라는 정수형 값으로 특정 위치에 있는 배열의 요솟값에 접근할 수 있습니다. 따라서 찾고싶은 요솟값의 인덱스값을 알고있다면 O(1) 로 해당 요솟값에 접근할 수 있습니다. 하지만 삭제와 삽입에는 해당 인덱스의 값에서 뒤쪽에 있는 값들을 한칸씩 땡기거나(삭제) 밀어야(삽입) 합니다. 따라서 삭제와 삽입을 할 때 최악의 경우 O(n)의 비용이 발생합니다.
LinkedList
연결리스트는 각각의 요소들이 다음 요소에 대한 위치값을 가지고 있습니다. 리스트의 데이터는 요소 또는 노드 라고 합니다.
노드 하나에는 데이터와 다음 노드를 가지고 있습니다. 예를들어
Class Node<T> {
private E data; // 노드가 가지는 데이터
private Node<E> next; // 현재 노드가 가리키는 다음 노드
public Node(E data, Node<E> next) {
this.data = data;
this.next = next;
}
}
Node<Long> node1;
Node<Long> node2;
node1 = new Node<Long>(1, node2); // 1의 데이터를 가지며 node2를 연결하고 있는 노드 생성
node2 = new Node<Long>(2, node3); // 2의 데이터를 가지며 node3을 연결하고 있는 노드 생성따라서 데이터와 다음 노드를 가리키는 값을 변경하는 것으로 삭제와 검색을 O(1)의 비용으로 할 수 있습니다.
위만 보면 Array 보다 좋은것 같지만 LinkedList 역시 단점이 있습니다.
삭제와 검색을 하려면 원하는 위치를 LinkedList 의 첫번째 노드부터 쭉 검색해봐야 합니다. 이는 Array 와 달리 논리적 저장 순서와 물리적 저장 순서가 다르기 때문에 발생하는 문제입니다.
결과적으로 LinkedList 는 검색에도 O(n) / 삭제, 삽입에도 O(n) 의 비용이 발생합니다.
그럼에도 쓸모가 없는것은 아닙니다. LinkedList 는 Tree 구조에서 사용되었을 때 진가를 발휘합니다.
Stack and Queue
Stack
스택이란? 데이터를 일시적으로 저장하기 위한 데이터 구조(선형 자료 구조) 입니다.
후입선출(Last In First Out) 즉, 가장 나중에 들어온 데이터가 가장 먼저 나옵니다.
차곡차곡 쌓이는 구조로 제일 먼저 들어간 데이터가 가장 바닥(Bottom)에 위치하고 그 위로 추가하는(Push) 데이터가 쌓입니다. 가장 나중에 추가한 데이터가 꼭대기(Top)에 위치하고 호출할 때(Pop) 꺼내지게 됩니다.

Queue
큐란? 데이터를 일시적으로 쌓아두기 위한 구조(선형 자료 구조) 입니다.
선입 선출(First In First Out) 즉, 가장 먼저 들어온 데이터가 제일 먼저 나옵니다.
Stack 과 반대로 가장 아래쪽에 있는 데이터가 호출됩니다.
큐에서는 데이터 꺼내는 맨 앞쪽을 프런트(front)라 하고, 데이터를 넣는 맨 뒤쪽을 리어(rear) 라고 합니다.
평소에 맛집에서 줄을 서있는 모습을 생각하시면 됩니다.
Java Collection 에서 Queue 는 인터페이스 입니다. 이를 구현하고 있는 PriorityQueue 또는 LinkedList 와 같은 클래스등
을 사용할 수 있습니다.
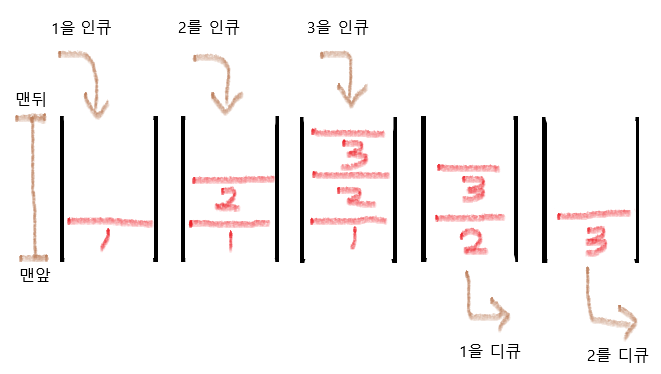
위의 그림 처럼 큐를 만들면 디큐 할 때 모든 요소를 한칸씩 앞으로 옮겨야하기 때문에 복잡도는 O(n) 이 됩니다.
때문에 다음처럼 링 버퍼로 큐를 만든다면 시간 복잡도를 O(1)로 만들 수 있습니다.
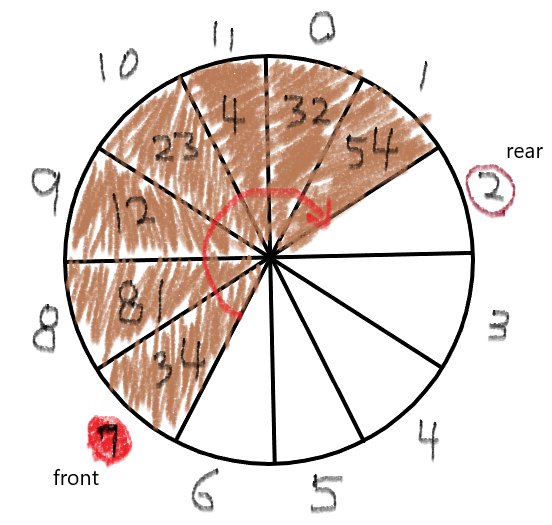
이렇게 큐를 구현하면 디큐 할 때 front 만 증가시킴으로써 더이상 한칸씩 이동시키지 않아도 됩니다.
따라서 처리 복잡도는 O(1) 이 됩니다.
Sort
대소 관계에 따라 데이터 집합을 일정한 순서로 줄지어 늘어서도록 바꾸는 작업을 말합니다.
내부 정렬 : 정렬할 모든 데이터를 하나의 배열에 저장할 수 있는 경우에 사용하는 알고리즘
외부 정렬 : 정렬할 데이터가 너무 많아서 하나의 배열에 저장할 수 없는 경우에 사용하는 알고리즘
정렬 알고리즘의 핵심 요소는 교환, 선택, 삽입
버블 정렬(Bubble sort)
- 배열이 제일 끝에서 부터 앞쪽으로 스캔하면서 이웃하는 두 요소를 비교하고 교환합니다.
- 요솟값을 비교하는 횟수는 n(n-1) / 2 회 입니다.
- 서로 이웃한 요소를 교환하기 때문에 안정적입니다.
단순 선택 정렬(Straight Selection Sort)
- 가장 작은 요소부터 정렬하는 알고리즘 입니다.
- 배열 {6, 4, 8 , 3, 1, 9, 7} 이 있으면 값이 1인 요소를 선택해 정렬을 시작합니다.
- 요솟값을 비교하는 횟수는 (n²-n) / 2 회 입니다.
- 서로 떨어진 요소를 교환하기 때문에 안정적이지 않습니다.
단순 삽입 정렬 (Straight Insertion Sort)
- 값이 가장 작은 요소를 선택해 그보다 더 앞쪽의 알맞은 위치에 삽입하는 작업을 반복합니다.
- 다시 말해서 선택한 요소의 자리부터 시작해서 앞쪽의 요소들을 한칸씩 뒤로 당기면서
- 선택한 요소보다 작은 값을 만났을 때 그 바로 뒤의 자리에 삽입하는 것입니다.
- {1, 2, 3, 8, 6, 4, 9} 가 있으면 4를 선택했을 때 {1, 2, 3, 4, 8, 6, 9} 가 되는것입니다.
- 단순 삽입 정렬의 비교 횟수와 교환 횟수는 n² / 2 회 입니다.
버블 정렬, 단순 선택 정렬, 단순 삽입 정렬의 시간 복잡도는 모두 O(n²) 로 효율이 좋지 않습니다.
셸 정렬(ShellSort)
- 단순 삽입 정렬의 장점은 살리고 단점은 보완하여 좀 더 빠르게 정렬하는 알고리즘 입니다.
- 먼저 정렬할 배열의 요소를 그룹으로 나눠 각 그룹별로 단순 삽입 정렬을 수행하고, 그 그룹을 합치면서 정렬을 반복하여 요소의 이동 횟수를 줄이는 방법입니다.
- 예를들어 {6, 4, 8, 3, 1, 9, 7, 5} 가 있다면 첫 요소부터 4칸만큼 떨어진 요소끼리 그룹을 만들어 정렬합니다.
- {6, 1} / {4, 9} / {8, 7} / {3, 5} ---> {1, 6} / {4, 9} / {7, 8} / {3, 5} ---> {1, 4, 7, 3, 6, 9, 8, 5}
- 다음은 2칸씩 떨어진 요소 마지막으로 1칸씩 떨어진 요소 끼리 적용하면 정렬을 마치게 됩니다.
- 셸 정렬의 시간 복잡도는 O(n 의 1.25승) 으로 빠르긴 하지만 멀리 떨어진 요소를 교환해야 하므로 불안정합니다.
퀵 정렬(Quick Sort)
일반적으로 사용되는 아주 빠른 정렬 알고리즘 입니다.
- 한 요소를 선택해 요소를 기준으로 [선택 요소보다 작은 그룹] / [선택 요소보다 큰 그룹] 으로 나눠 정렬합니다.
- 배열을 두 그룹을 나눈 뒤 다시 그룹 안에 한 요소를 기준으로 그룹을 나눠 하나의 요소만 남을 때 까지 정렬합니다.
- 스택을 사용해서 정렬 할 수 있으며 시간 복잡도는 O(n log n) 입니다.
- 다만 정렬할 배열의 초깃값이나 피벗의 선택 방법에 따라 시간 복잡도가 증가하는 경우도 있습니다.
- 예를 들어 매번 단 하나의 요소와 나머지 요소로 나누어지면 n번의 분할이 필요해 최악의 시간 복잡도는 O(n²)입니다.
병합 정렬 (Merge Sort)
- 배열을 앞부분과 뒷부분으로 나누어 각각 정렬한 다음 병합하는 작업을 반복하여 정렬을 수행하는 알고리즘 입니다.
예를들어 {1, 2, 21, 4, 3, 16, 11, 6, 4, 2, 8, 1, 13} 라는 배열이 있다면 배열의 가운데를 기준으로
배열 A = {1, 2, 21, 4, 3, 16} / 배열 B = {11, 6, 4, 2, 8, 13} 앞 배열과 뒷 배열로 나눕니다.
{1, 2, 3, 4, 16, 21} / {2, 4, 6, 8, 11, 13} 두 배열을 각각 정렬하고
여기서 pa, pb, pc 라는 각 배열의 커서 변수를 만들고 모두 0으로 초기화 합니다.
A[0] = 1 ,B[0] = 2 A[0]이 더 작으므로 A[0]를 병합용 배열 C에 넣고 pa, pc 를 1씩 증가시킵니다. 배열 C -> {1}
계속해서 A[pa] 와 B[pb] 값을 비교하며 배열C에 병합 시켜주면 정렬이 완성됩니다.
- 병합 정렬의 시간 복잡도는 O(n log n) 입니다.
- 병합 정렬은 서로 떨어져있는 요소를 교환하는 것은 아니므로 안정적인 정렬 방법입니다.
자바의 Arrays.sort 메서드는 기본 자료형 배열의 정렬인 경우는 퀵 정렬을 사용하고
클래스 객체 배열의 정렬일 경우 병합 정렬을 사용합니다.
힙 정렬(Heap Sort)
힙 이란?
부모의 값이 자식의 값보다 항상 크다 or 항상 작다 라는 조건을 만족하는 완전이진트리 입니다.
완전이진트리란?
완전이진 상태의 트리를 말하는 것입니다. 여기서 '완전' 이란 부모는 자식을 왼쪽부터 추가하는 모양을 의미합니다.
'이진' 이란 부모가 가질 수 있는 자식의 최대 개수는 2개 라는 뜻입니다.
힙 정렬은 '가장 큰 값이 루트에 위치' 하는 특징을 이용하는 정렬 알고리즘입니다.
힙에서 가장 큰 값인 루트를 꺼내고 다시 힙상태를 만든뒤 다시 루트를 꺼내는것을 반복하여 정렬하는 방법입니다.
시간복잡도는 가장 큰 요소를 선택할 때의 O(1) 이며
대신 힙 정렬에서 다시 힙으로 만드는 작업의 시간 복잡도는 O(log n) 입니다.
도수 정렬 (Fsort)
도수 정렬이란?
요소의 대소 관계를 판단하지 않고 빠르게 정렬할 수 있는 알고리즘 입니다.
도수 정렬 알고리즘은 도수분포표 작성, 누적도수분포표 작성, 목적 배열 만들기, 배열 복사
도수 정렬을 하기 위해서 요솟수, 배열의 요소중 최대값 or 최솟값을 미리 알고 있어야합니다.
이중 for문없이 for문으로만 정렬할 수 있기 때문에 상당히 깔끔합니다.
'생각정리' 카테고리의 다른 글
| [우아한테크코스3기] 레벨1 회고 (feat. 레벨2 다짐하기) (1) | 2021.04.11 |
|---|---|
| [2021.03.24] 우아한테크코스 한 달 생활기 (0) | 2021.03.26 |
| [기술면접 시리즈] 자바의 컴파일 과정(JVM 메모리 구조) (0) | 2020.08.03 |
| [기술면접 시리즈] 시작. (0) | 2020.08.03 |
| 단위테스트의 필요성에 대해서 (0) | 2020.07.24 |



댓글